基于PSpice System Option接口的直流电机控制系统设计

本文将用实例的方式演示以分段建模的方式优化直流电机控制系统。

下面是直流电机控制系统的示意图：

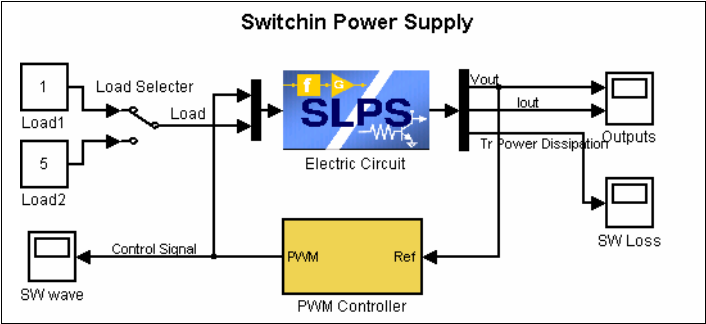
图1 直流电机控制系统

该图由定子或励磁绕组组成，该绕组产生恒定的励磁磁通量。该绕组由电感Ls和电阻Rs建模。当电压Vs施加到定子绕组时，电流is流动，产生磁通Ψ。转子绕组也通过其电感L_R和电阻R_R来建模。当电压V_R施加到转子绕组时，电流I_R流动。V_R是由差分输入电压V_D驱动的控制器的输出。信号流是从V_D到V_R，但不是在相反的方向上。因此，转子和定子之间的电枢反作用被忽略。

首先，我们写出定子绕组的数学方程式：

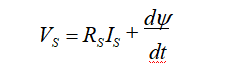
通常，磁通量Ψ是定子电流I_s的非线性函数。为了简单起见，我们假设Ψ是I_s的线性函数：

y = LS IS

因此我们可以得到： 

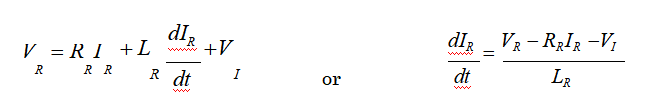
对于转子绕组的数学方程，我们得到

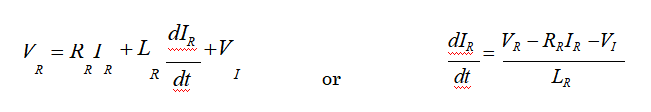
V_I是当转子绕组在励磁场中旋转时在转子绕组中感应的相反的电动势。V_I可以写成常数C₁、通量Ψ和角速度ω的乘积。

V₁ = C₁yw

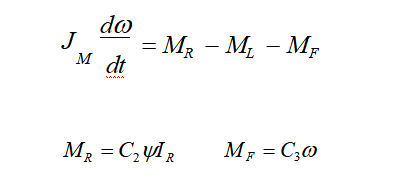
控制器由设置的标称角速度ω_S的速度电位器电压和与角速度ω成正比的转速表电压之间的电压差V_D驱动。我们可以将V_D写成角速度之差乘以常数C₄：

V_D = C₄ (ω_S –ω )

对于控制器，我们使用PI特性，其描述如下：

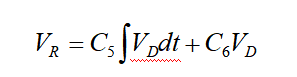
首先，我们在Simulink中对整个系统进行建模。

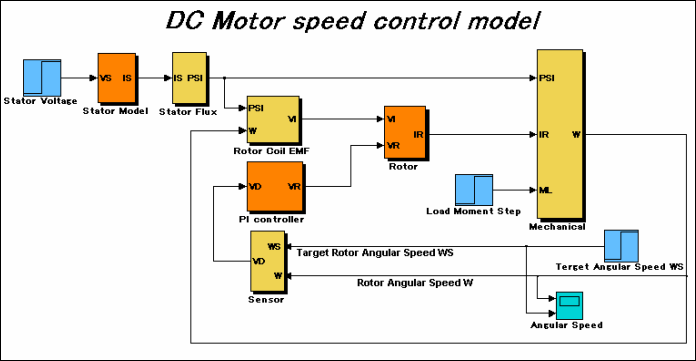
图2  Simulink 模型

角速度ω_S（t）和ω（t）的曲线如下所示。定子电压V_S在时间t＝1s处被接通。ω_S在2s时设置为50 rad/S，转子开始转动。在t=6s左右，ω达到50 rad/s的稳态。

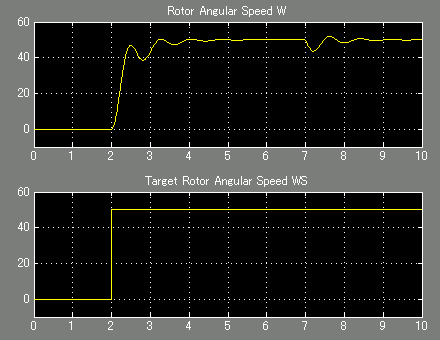
图3. Angular velocitiesω(t) and ωS(t)

参考Simulink模型的仿真结果，我们现在将把一些Simulink块替换为PSpice电路。下面是系统框图

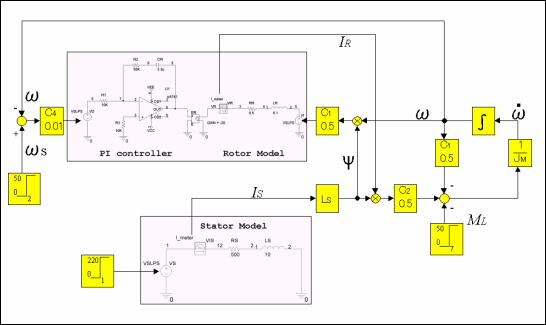
图4. 系统框图

下面是Simulink模型，其中包括使用SLPS的PSpice电路。

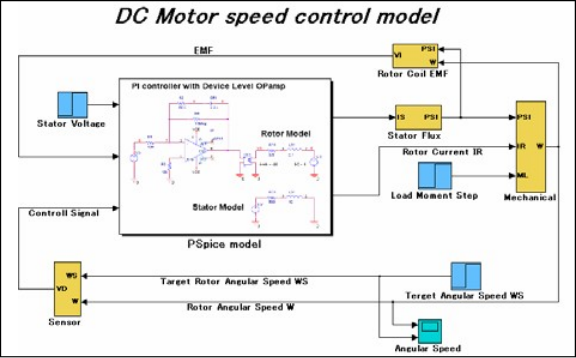
图5. Simulink 模型

定子、转子和PI控制器采用PSpice建模，如下所示。

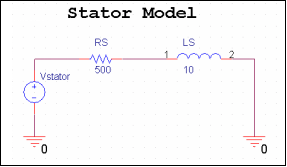
图6.定子电路

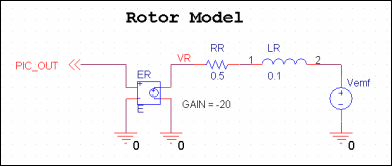
图7.转子电路

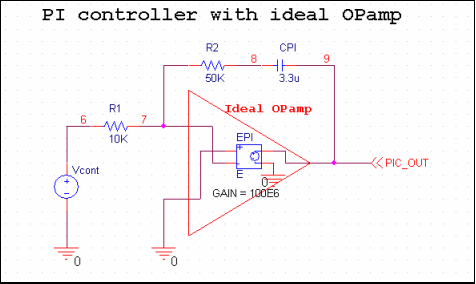
图8. PI 控制电路

电路元件V_S、R_S、L_S和E_R、R_R、L_R实现dI_s/dt和dI_R/dt的等式。对于PI控制器中的运算放大器，我们首先使用一个理想的模型，该模型具有很高的开环增益、无限输入电阻、零输出电阻、零输入偏置电压、零输入偏移和偏置电流，并且没有输出电压饱和。这种行为很容易在PSPICE中通过线性电压控制电压源进行建模。PI控制器输出电压V(9)（PIC_OUT）由以下等式给出。

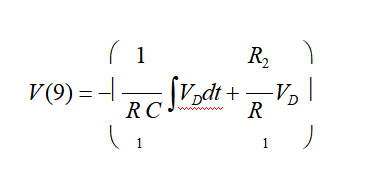
有了这些因素

I和P特性相交的角频率f0为：

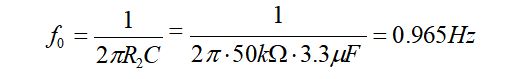
电压V(9)控制增益值为-20的电压控制电压源ER。因此，我们得到

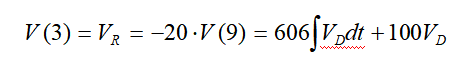
将此方程与Simulink模型中的V_R方程进行比较，我们注意到两者是相同的，因为常数C₅=606和C₆=100。因此，PSpice控制器电路在Simulink模型中实现了与子系统PI控制器相同的V_R方程。

仿真结果如下：

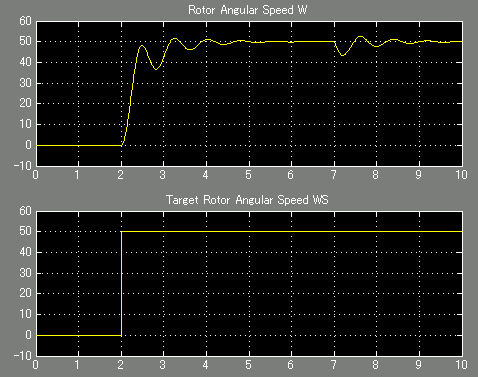
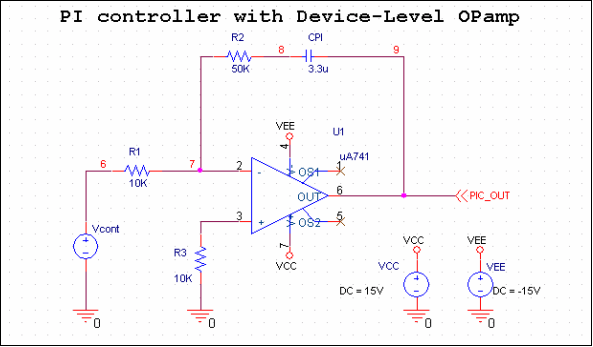
图10. 使用μA741的PI控制器电路

Simulink-PSpice 仿真结果（实际运放）

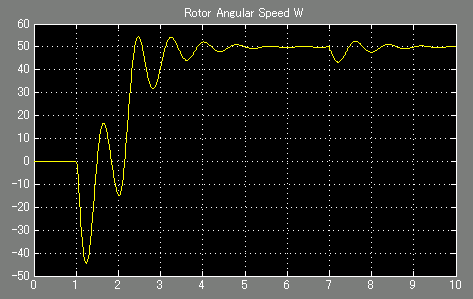
图11. 使用μA741的PI控制器的ω_S(t)

在1s点开启激励后，电机开始反向转动。显然，设备级模型的行为与控制器中使用的理想运放模型不同。这是因为在t=0直流工作点计算时，由于输入失调电压和非常高的开环增益，运放输出进入饱和状态。

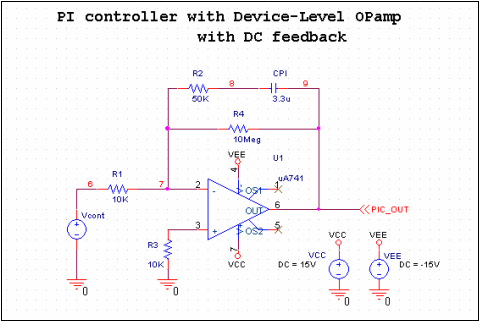
图12. 带直流反馈的PI控制电路

Simulink-PSpice 仿真结果（直流反馈）

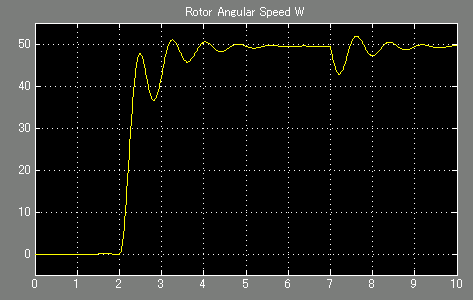
图13. ω_S(t)（R4=10MΩ）

由于运放输出偏置电压降低，相反方向的初始瞬态也降低。直流增益降低的负面影响是ω(t)的稳态响应与50 rad/s略有不同。

通过在设计过程的每个阶段选择不同的模型，您可以快速查找并解决问题。首先用理想模型建模，就可以确定近似参数。然后，您可以将这些理想模型替换为线性电子元件，然后再替换为非线性器件，以进行最终电路验证。在Simulink中使用PSpice (SLPS)可以减少设计修改的次数，并使您的设计周期更短。