详解时域瞬态分析技术

2022-02-16
2:42 下午

本文要点：

所有的物理系统在运行动态中都会表现出一些瞬态行为，电子产品也是如此
瞬态分析技术可以帮助了解不同电气状态之间的转换
当检查测量数据或软件仿真数据时，一些基本的瞬态分析技术可用于了解电气状态之间的转换

当打开或关闭 LED 时，随着光线变亮或变暗有一个缓慢的过渡。这种类型的瞬态行为非常简单，但这是一个电子系统改变状态时的基本反应。使用瞬态分析可以充分理解时域中的信号转换，以及它们与重要系统参数的关系。

初次接触软件仿真数据的设计师可能认为时域瞬态分析是一个简单、只是在图表上观察波形的问题。但实际情况是，瞬态分析中需要用到一系列的数学技术和商业软件应用。通过一些创造性的方法和强大的设计工具，可以全面了解电子产品的瞬态行为。这往往不需要手动完成大量计算，直接观察时域响应和一些简单的数学步骤即可获得重要的见解。

时域瞬态分析技术在时域中运用，全面展现了不同状态之间的信号转换过程。

如何进行时域瞬态分析

瞬态分析涉及一套技术，用于分析时域中的仿真数据或实验结果，特别是当所研究的系统在两个状态之间过渡时。举例而言，此时我们有一个已经充电到 5V 的 RC 电路：如果源电压突然变为 7V，在时域中就会出现这两种状态的过渡。时域瞬态分析的一些原则方法包括：

稳定性分析：这是对拉普拉斯域分析（Laplace domain analysis）的概括，但它可以应用于耦合的非线性系统，这些系统可能表现出不稳定的瞬态行为。稳定性分析使用一系列的技术来预测系统在哪些条件下会有稳定的瞬态响应。
参数提取：这类回归技术被用来确定分析模型中的参数。这是通过比较模型预测和测量数据来完成的，然后应用统计技术来判断预测和实验数据的一致程度。
建立经验模型：总结性瞬态分析的一种方法是根据实验或现场求解器数据建立经验模型。经验模型非常适合快速预测系统的行为或寻找不同复杂度的模型之间的一般关系。这些模型甚至已经被纳入 IPC 标准。

下图显示了当负载吸取一个电流脉冲（例如一个开关数字电路）时，一些典型的LDO 稳压器输出电压的实验数据。可以通过瞬态分析来研究输出电压的下降，从而修改电路以提供更稳定的输出电压。

LDO 稳压器的瞬态响应示例，显示了电压下降和恢复情况

瞬态分析中一些可能的检查点包括建立稳定时间（或恢复时间），以及这与稳压器中的各种参数的关系。在许多系统中，少数特定参数将负责确定系统的瞬态响应，但可能缺少分析模型来描述这种关系。

参数提取

很多时候，我们有一个理论的系统模型，需要从测量数据中提取模型的参数。有许多方法可以做到这一点，取决于模型的形式以及是否有一个分析解决方案。这些方法一般分为两个方面：

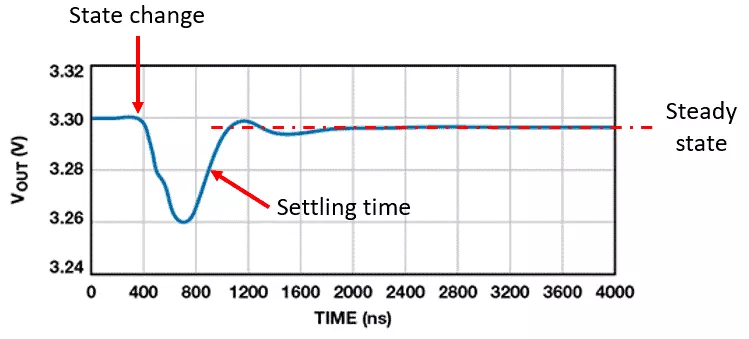
回归：如果描述系统的分析模型是已知的，那么它可以用于回归分析，以确定任何未知的模型参数。
统计比较：有时，系统的分析模型并不为人所知，但可能有一个数字模型，例如来自场求解器的模型。在这种情况下，场求解器的结果可以针对各种系统参数值产生，两个数据集可以进行统计比较，以确定最可能的系统参数值。

稳定性分析

拉普拉斯变换和拉普拉斯域中的函数经常用来描述物理系统的瞬态行为。稳定性分析涉及建立在拉普拉斯域上的一套更完整的技术。在线性时变 (linear time-invariant ，即LTI) 系统中，包括在耦合系统中，稳定性分析方法产生的结果与拉普拉斯变换求解技术相同。在线性系统的稳定性分析中，目标是解出以下特征值方程：

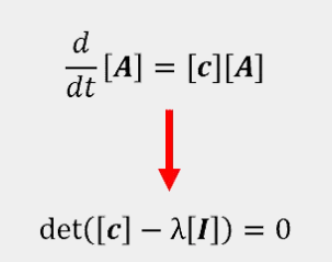
用于稳定性分析和瞬态分析的主特征方程

特征值 (λ) 的实部和虚部以复数共轭对的形式出现，用于表明系统的极点和零点。借此，我们可以立即知道系统是否有稳定的响应、在接近稳定状态时是否会有瞬态振荡（极限周期），以及系统接近稳定状态的速度。下表总结了线性系统中各种 λ 值的预期瞬态行为。

对于非线性系统来说，确定稳定性的方法并不单一，一系列可能的方法都可以应用于不同的系统。暴力的时域仿真可以给出一些有用的结果，这也是 SPICE 求解器中用于非线性电路的主要方法。这仍然是一个活跃的研究领域，稳定性方法往往需要针对特定的非线性系统进行调整，以获得实用的见解。

建立经验模型

这是最普遍的瞬态分析形式，因为它只是使用线性或非线性回归将建议的模型方程与实验数据相匹配。如果有 MS Excel 或其他电子表格程序，就可以为系统创建一个经验模型，并在任何其他分析中加以使用。一流电子电路仿真器可以直接从数据中建立一个模型，并从结果中创建一个 SPICE 子电路，然后可以将其纳入更大的电路中。电子学的经验建模需要使用正确的设计和仿真应用，来帮助实现瞬态分析的自动化。